Hence this median is also the altitude. The altitude median angle bisector and perpendicular bisector for each side are all the same single line.
The Altitude Of An Equilateral Triangle Is 6 Inches Long What Is The Length Of A Side Of The Triangle What Triangles Are Formed By The Altitude Quora
If we know the three sides a b and c.
. ANSWER 214 views View upvotes View 4 shares Related Answer. It also forms two equivalent right-angled triangles. For an equilateral triangle median angular bisector and altitude will be same between a selected pair of point and side.
This implies that the altitude from this vertex must bisect the opposite side. Side2 3 to calculate the height. Also the altitude of an isosceles triangle when measured.
If median drawn from vertex A is also the angle bisector the triangle is isosceles such that AB AC and BC is the base. Area ½ x a x 3a2. An altitude of an equilateral triangle is also an angle bisector median and perpendicular bisector.
Every triangle has three altitudes h a h b and h c each one associated with one of its three sides. Since the altitudes are the angle bisectors medians and perpendicular bisectors point. In Figure 2 AC is an altitude to base BC and BC is an altitude to base AC.
It bisects the base of the triangle and always lies inside the triangle. 632 33 units is the length of the altitude. The altitude forms a right triangle in which it is adjacent to an angle of 30 and is therefore equal to 32 of the hypotenuse which is 6 units.
Yes the altitude of a triangle is a perpendicular line segment drawn from a vertex of a triangle. For any triangle with sides a b c and semiperimeter s a b c 2 the altitude from side a is given by This follows from combining Herons formula for the area of a triangle in terms of the sides with the area formula 12baseheight where the base is taken as side a and the height is the altitude from A. So if the altitude of an equilateral triangle is.
Because the equilateral triangle is in some sense the simplest polygon many typically important properties are easily calculable. Find the area of a equilateral triangle with a side of 8 units. Plug height into the area formula 12b h.
An equilateral triangle has three equal sides and angles. In Figure 3 AM is the altitude to base BC. In an equilateral triangle each altitude median and angle bisector drawn from the same vertex overlap.
For instance for an equilateral triangle with side length. This line will also be. It can also be understood as the distance from one side to the opposite vertex.
Area of an Equilateral Triangle. Use the height formula. Equilateral triangles have sides of equal length with angles of 60.
Altitudes of equilateral triangles. An altitude from a vertex bisects the opposite base if and only if the two sides emerging from that particular vertex are equalnot necessary in a right angle triangleTherefore you need to specify this condition before assuming that the altitude cuts. As it is altitude it will be perpendicular always.
Yes - the altitude of an equilateral triangle is perpendicular to the side chosen as the base and bisects that side and the opposite angle. To find the height we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles. In an isosceles triangle a triangle with two equal sides if the altitude is constructed towards the non-equal side it will cut that side perfectly in half.
The three altitudes of an equilateral triangle intersect at a single point. So for a right triangle using Pythagoras theorem we can write. Area ½ x a x 3a2.
Altitudes can sometimes coincide with a side of the triangle or can sometimes meet an extended base outside the triangle. A 2 h 2 a2 2 or h 2 a 2 a2 2 3a 2 4 h 3a2 By putting this value in equation 1 we get. Now the side of the original equilateral triangle lets call it a is the hypotenuse of the 30-60-90 triangle.
ADC and CDB are equal because the have two sides equal and one angle equal SAS then ADDB hence the altitude bisects the base. Try to prove all these properties on your own. An altitude from a vertex bisects the opposite base if and only if the two sides emerging from that particular vertex are equalnot necessary in a right angle triangle.
So for a right triangle using Pythagoras theorem we can write. Now from the above figure the altitude h bisects the base into equal halves such as a2 and a2. Altitude is also a bisector.
The legs of either right triangle formed by an altitude of the equilateral triangle are half of the base a and the hypotenuse is the side a of the equilateral triangle. Up to 10 cash back Correct answer. Height 82 343.
The altitude of a triangle or height is a line from a vertex to the opposite side that is perpendicular to that side. A perpendicular line can drawn from the top point of the triangle to the base where it will bisect the base to form two congruent right triangles. Therefore the altitude and median from this vertex must coincide.
Now from the above figure the altitude h bisects the base into equal halves such as a2 and a2. In an equilateral triangle all angles are 60. As in any type of triangle its area is equal to half of the product of its base and height.
Therefore the sides opposite the equal angles are the same length. CD is the altitude from vertex C to base AB. Consequently this vertex must be on the perpendicular bisector of the opposite side.
A 2 h 2 a2 2 or h 2 a 2 a2 2 3a 2 4 h 3a2 By putting this value in equation 1 we get. Does the Altitude of a Triangle Always Make 90 With the Base of the Triangle. Figure 3 An altitude for an obtuse.
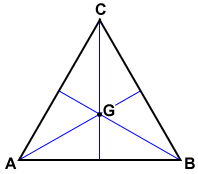
The height of an equilateral triangle can be found using the Pythagorean theorem so that. The three altitudes extending from the vertices A B and C of ABC above intersect at point G. The area it will be defined by the following formula.
From what I deduced from Wikipedia is that this is only true if the triangle is either isosceles or a right triangle is not fully correct. Therefore you need to specify this condition before assuming that the altitude cuts the opposite base in half. Figure 2 In a right triangle each leg can serve as an altitude.
Does an altitude always bisect the opposite side of a triangle. And so on III. It also forms two equivalent right-angled triangles.
What Is The Altitude Of Any Equilateral Triangle Quora
Does The Altitude Of A Triangle Always Bisect The Base Of Any Type Of Triangle Or Are There Any Conditions Quora

What Is Altitude Of A Triangle Definition Formulas And Examples
0 Comments